
출처 : 프로그래머스, https://school.programmers.co.kr/learn/courses/30/lessons/12902
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
먼저, 생각해야 할 부분
1. 익숙하다. 2 x n 타일링에서 많이 보았다.
DP에서 한 단계로 묶일 수 있는 것이 무엇이 있는가 생각해보자.
3 x n이므로 입력으로 홀수는 들어올 수 없다. 즉, n은 짝수만 가능하다.
2. 점화식을 제대로 구하는 것이 중요하다.
예제를 살펴보면서 채울 수 있는 형태가 어떤 것이 있는지 고려해보자.
풀이
def solution(n):
n //= 2
dp = [1 for _ in range(n+1)]
for i in range(1, n + 1):
dp[i] = (3 * dp[i-1] + 2 * sum(dp[:i-1])) % 1000000007
return dp[n]
3 x n이므로 입력에 홀수는 들어올 경우 블록으로 가득 채울 수 없다.
즉, n은 짝수만 가능하다. = 한 단계가 짝수만큼 증가하도록 구성된다.
다시 말해, 이전 단계는 짝수만큼 빼면 된다.
이를 바탕으로 점화식을 찾아보자.
- F(n-2)

먼저 2칸 전의 경우이다.
2칸 전까지의 경우 F(n-2)에서 새롭게 2칸을 추가하여 F(n)을 만들 수 있다.
이 때, 들어갈 수 있는 2칸의 경우의 수는 3개이므로, F(n) = 3 * F(n-2) ..... 이다.
- F(n-4)

4칸 전의 경우인 F(n-4)를 살펴보자.
F(n-4)에서 블록을 이용해 F(n)을 만들 수 있는 4칸짜리 블록 모음은 위의 2개이다.

물론 위와 같은 방식으로도 4칸짜리 블록 모음을 만들 수 있다.
그러나 자세히 살펴보면 이는 2칸 짜리 블록 모음 2개로 나눌 수 있고 F(n-2)와 겹친다는 것을 알 수 있다.
F(n-2)와 겹치지 않으려면 중간의 블록이 가로로 뉘어져 있는 방식이어야만 하는데 이 경우의 수는 2가지 밖에 없다.
즉, F(n) = 3 * F(n-2) + 2 * F(n-4) + .....이다.
- F(n-6)
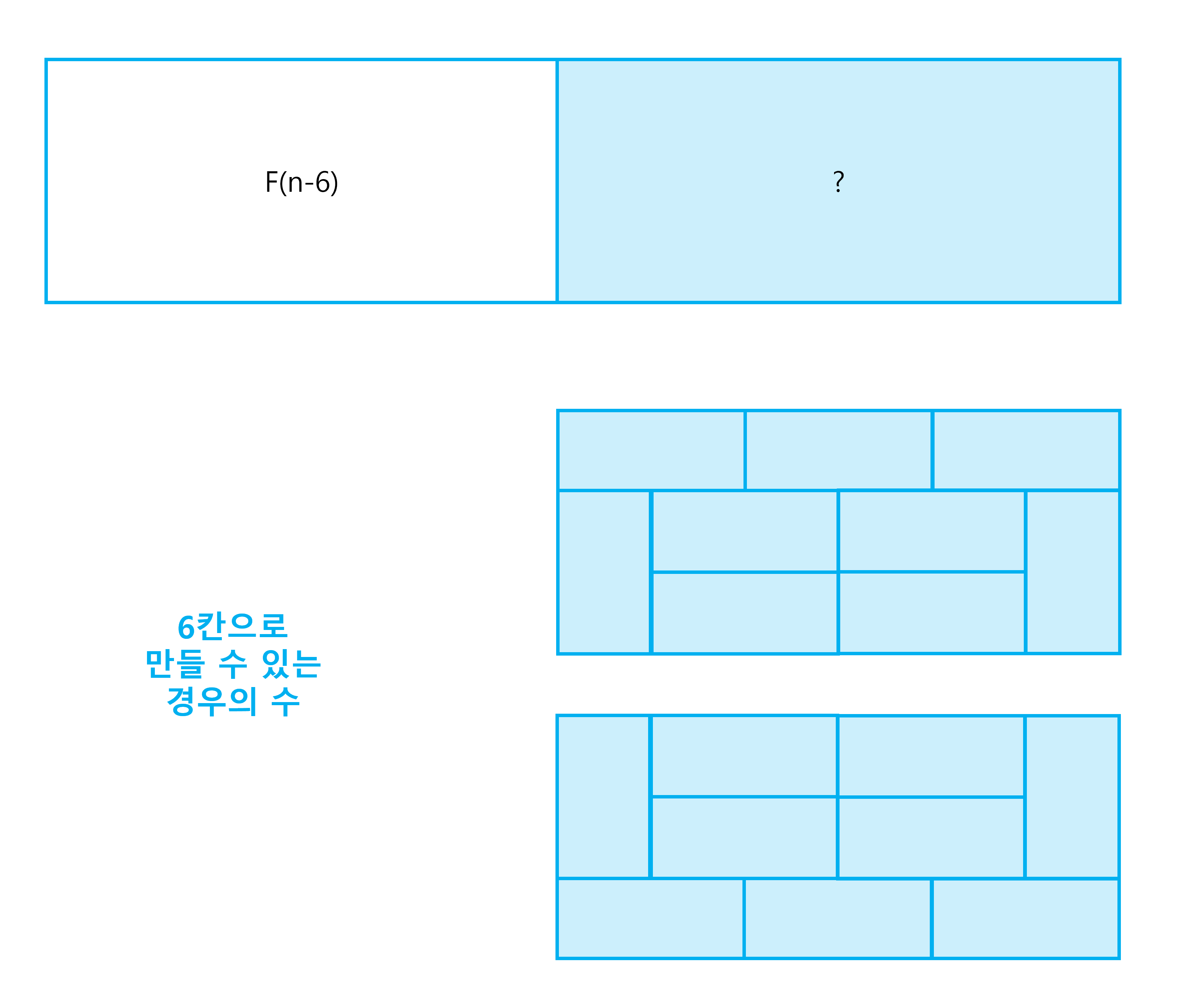
6칸 전으로 가보자.
F(n-4)에서 2칸 단위로 나뉘지 않도록 블록을 만들어야 F(n-2)와 겹치지 않는 방식으로 채울 수 있다는 것을 알았다.
이를 F(n-6)에도 적용시켜보면,
위의 2가지 경우 외에는 4칸, 2칸으로 나뉘거나 2칸, 2칸, 2칸으로 나뉜다는 것을 알 수 있다.
즉, F(n) = 3 * F(n-2) + 2 * F(n-4) + 2 * F(n-6) ....이다.
여기서 생각을 조금 더 확장시켜보면, n-4부터는 양 끝 블록 2개를 제외하고 전부 뉘어져 있는 형태만이 가능하므로
2가지 방법 외에는 모두 겹치게 된다는 것을 알게 된다.
결론적으로, F(n) = 3 * F(n-2) + 2 * sum(F(n-4) + F(n-6) + F(n-8) + .....)이다.
이를 코드로 작성하면 위의 풀이와 같다.
시간 복잡도
O(N)
알게 된 점
-
고찰
블록 찾기 어렵다.......
Github
'알고리즘 > Python' 카테고리의 다른 글
| [python] 프로그래머스 - 최솟값 만들기 (0) | 2022.07.17 |
|---|---|
| [python] 프로그래머스 - 숫자 블록 (0) | 2022.07.15 |
| [python] LeetCode #1 - Two Sum (0) | 2022.07.13 |
| [python] 백준 14430 - 자원 캐기 (0) | 2022.07.10 |
| [python] 백준 10164 - 격자상의 경로 (0) | 2022.07.10 |
