다익스트라(Dijkstra) 알고리즘
다익스트라 알고리즘은 그래프의 한 노드에서 모든 노드까지의 최단 거리를 구하는데 사용됩니다.
플로이드 워셜 vs 다익스트라
플로이드 워셜은 모든 노드에서 다른 모든 노드까지의 최단 거리를 구하는 용도인 반면,
다익스트라는 시작점을 1개의 노드로 정하고 이 노드로부터 다른 모든 노드까지의 최단 거리를 구합니다.
BFS vs 다익스트라
BFS와 다익스트라 모두 최단 거리를 구하기 위한 알고리즘으로 사용될 수 있습니다.
단, BFS는 가중치가 없는 그래프인 경우에 최단 거리 문제를 푸는 방법이고,
다익스트라는 가중치가 다양한 경우에 최단 거리 문제를 푸는 방법입니다.
가중치가 없는 경우 모든 칸에 대해서 1번 이동하는 것이 동일한 가중치를 가진다 볼 수 있기 때문에,
가장 먼저 나오는 경로가 최단 거리가 됩니다.
하지만, 가중치가 있을 경우 가장 먼저 나온다고 하더라고 가중치에 따라 최단 거리가 아닐 수 있습니다.
때문에, 가중치가 없는 경우 BFS를, 가중치가 다양한 경우 다익스트라를 사용하여 풉니다.
원리
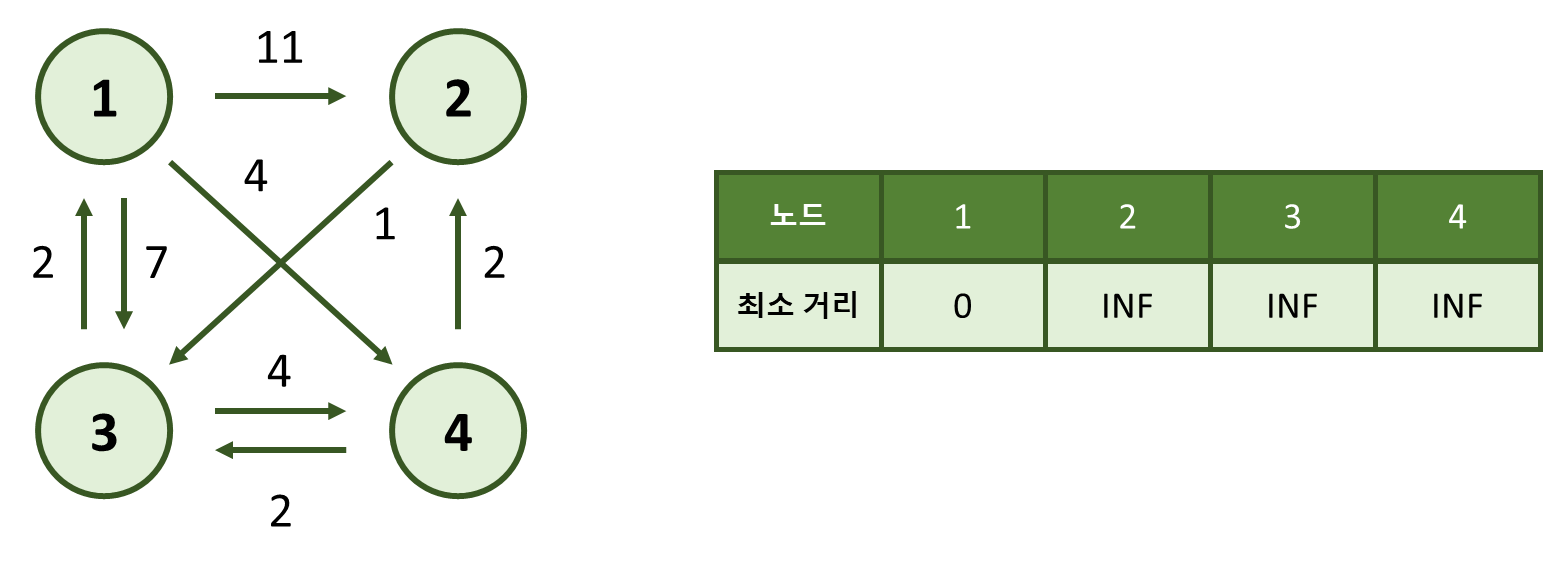
다음과 같은 그래프가 있습니다.
이 그래프에서 시작 노드를 1번 노드로 잡겠습니다.
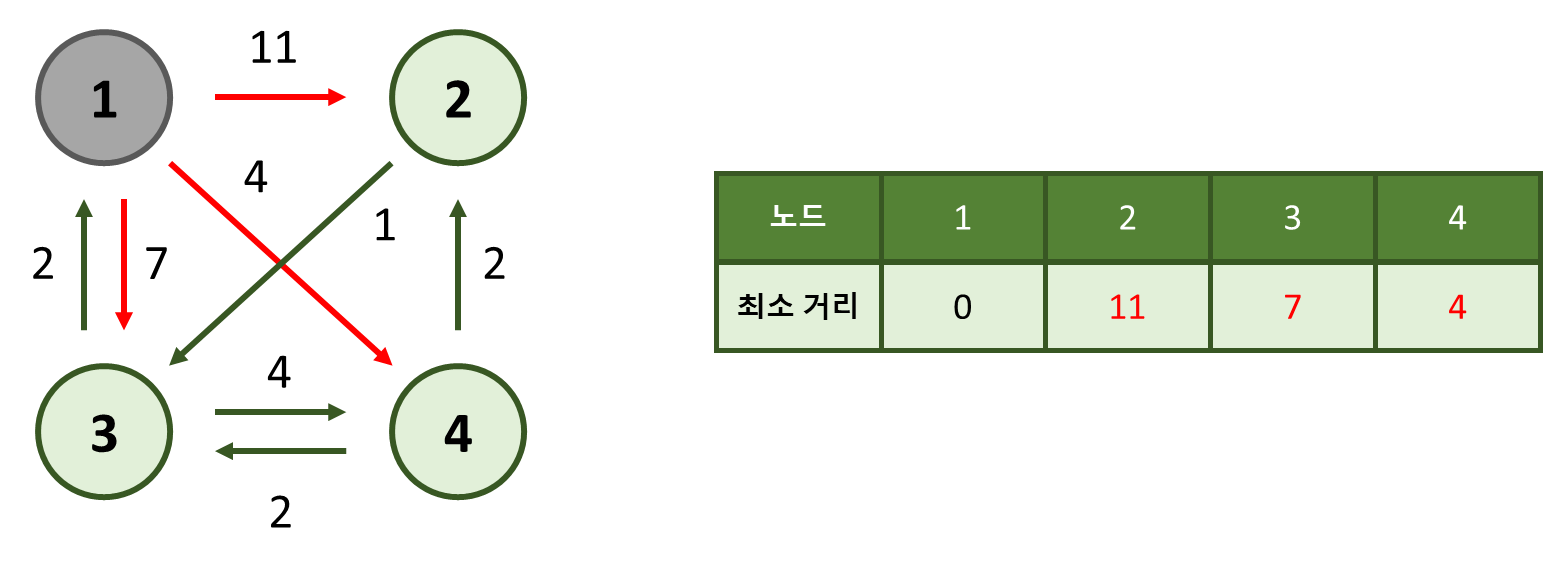
1번 노드에 인접한 노드들에 대해 최소 경로를 업데이트해줍니다.
이제 1번 노드를 제외한 나머지 노드 중 최소 거리인 노드를 찾습니다.
이 경우, 최소 거리가 4인 4번 노드가 해당하는 노드가 됩니다.
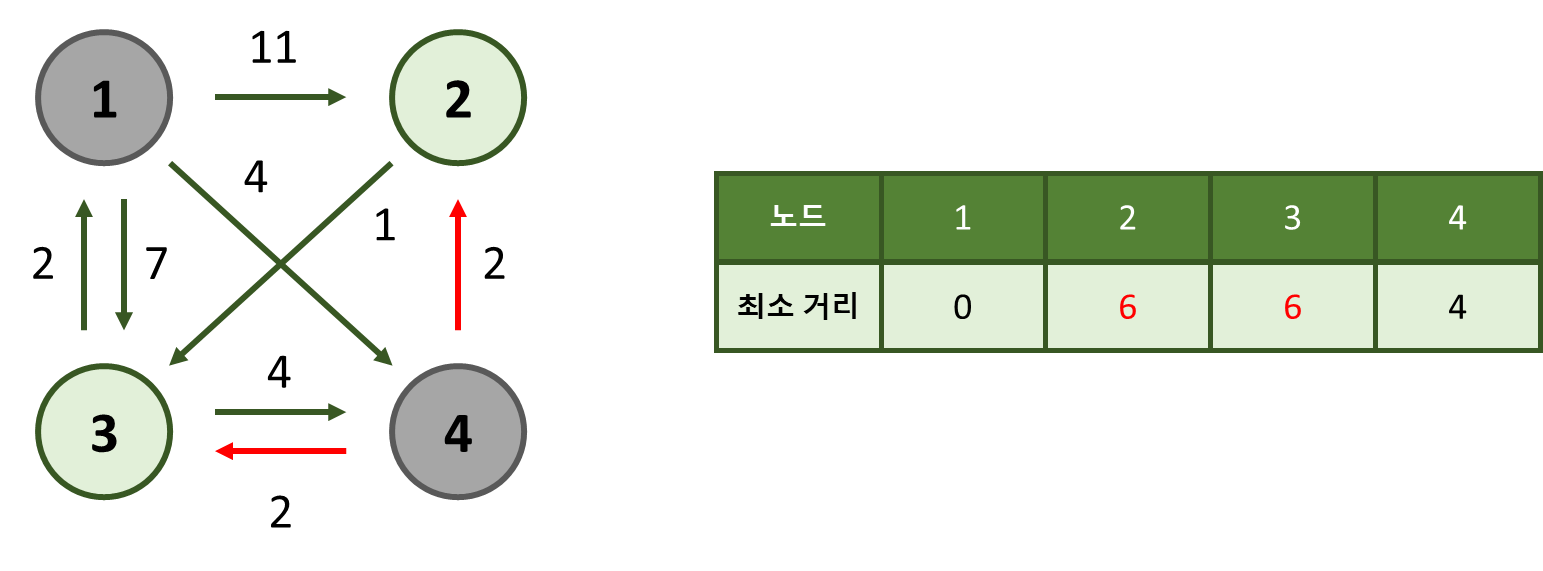
4번 노드부터 인접한 노드들에 대해 최소 거리를 업데이트 해줍니다.
2번 노드의 경우, 이전에 최소거리가 11이었지만,
4 + 2 = 6 (4번 노드의 최소 거리 + 4번 노드에서 2번 노드로의 거리)으로 6으로 업데이트 됩니다.
마찬가지로 3번 노드 역시, 이전 최소거리 7에서, 4 + 2 = 6이 더 작으므로 이로 업데이트 됩니다.

1과 4를 제외한, 2번과 3번 노드의 최소 거리가 같으므로, 임의로 2번을 선택하겠습니다.
이 경우, 인접한 3번 노드에 대해 6 + 1 = 7인 거리를 계산할 수 있습니다만,
기존 3번 노드의 최소 거리가 6으로 7보다 작아 업데이트하지 않습니다.

마지막으로 남은 3번 노드를 선택합니다.
모든 노드를 방문했으므로 업데이트 할 노드가 없습니다.
따라서 다익스트라 알고리즘을 종료합니다.
코드화
다익스트라 알고리즘은 우선순위 큐를 이용해 코드로 작성할 수 있습니다.
정확히는 우선순위 큐의 우선순위를 최소 거리로 삼아
최소 거리가 가장 작은 노드를 찾는 과정을 우선순위 큐를 통해 간소화할 수 있습니다.
- 인접 행렬을 통한 코드화
n x n의 인접 행렬을 통해 그래프를 표현할 수 있습니다.
구현이 간단하지만, 이 경우 그래프 내의 노드가 많아지면, 인접행렬을 통해 최단 거리 갱신 시
필요 없는 성분들(연결되어있지 않은 노드: INF)까지 참조하게 되어 시간이 오래 걸릴 수 있습니다.
adjacency_matrix = [[INF for _ in range(n)] for _ in range(n)]
# 그래프 초기화
for v1, v2 in edge:
adjacency_matrix[v1][v2] = weight1
adjacency_matrix[v2][v1] = weight2
# ------------- 위 과정은 그래프 형태를 설명하기 위해 존재하는 코드 --------------
from heapq import heappop, heappush
INF = float('inf')
# 최소 거리 배열
min_distance = [INF for _ in range(NODE_COUNT)]
heap = []
# 방문 체크용 집합
visited_node = set()
# 시작 노드 0번째 노드로 설정
min_distance[0] = 0
heappush(heap, (0, 0))
while len(heap) > 0: #우선순위 큐가 빌 때까지 계속
# 큐에서 가장 짧은 최소 거리인 노드를 꺼낸다.
current_node_dis, node_idx = heappop(heap)
# 방문했다면, 패스
if node_idx in visited_node:
continue
# 방문 체크
visited_node.add(node_idx)
# 현재 노드의 거리 값 + 인접한 노드의 거리 값을 인접 노드까지 최소 거리로 업데이트
for near_node_idx in range(NODE_COUNT):
# 인접 행렬에서 현재 노드 -> 근접 노드 가중치를 찾는다.
near_node_dis = adjacency_matrix[node_idx][near_node_idx]
# 인접하지 않다면 패스
if near_node_dis == INF:
continue
# 인접한 노드에 한해 최소 거리 갱신
min_distance[near_node_idx] = min(min_distance[near_node_idx], current_node_dis + near_node_dis)
# 갱신된 최소 거리를 우선순위로 인접한 노드를 우선순위 큐에 넣음
heappush(heap, (min_distance[near_node_idx], near_node_idx))
- 인접 리스트를 이용한 코드화
인접 행렬의 문제점은 최단 거리 갱신을 위해 인접 노드 검색 시 연결되어있지 노드까지 검색한다는 점입니다.
이를 해결하기 위해서는 반대로 연결되어 있는 노드만 검색하도록 만들면 됩니다.
이는 그래프의 연결 관계를 인접 리스트로 만들어 해결할 수 있습니다.
from collections import defaultdict
adjacency_list = defaultdict(lambda: [])
# 그래프 초기화
for v1, v2 in edge:
adjacency_list[v1].append((v2, weight1))
adjacency_list[v2].append((v1, weight2))
# ------------- 위 과정은 그래프 형태를 설명하기 위해 존재하는 코드 --------------
# 다익스트라
# 최소 거리를 갱신하는 것
min_dis = [INF for _ in range(n)]
heap = []
visited_set = set()
# 다익 초기화
min_dis[0] = 0
heappush(heap, (0, 0))
while len(heap) > 0:
current_dis, current_node_idx = heappop(heap)
# 방문했다면 패스
if current_node_idx in visited_set:
continue
visited_set.add(current_node_idx)
# 인접 노드 최소 거리 갱신
for near_node, weight in ad_list[current_node_idx]:
min_dis[near_node] = min(min_dis[near_node], current_dis + weight)
# 힙에 넣자.
heappush(heap, (min_dis[near_node], near_node))
시간복잡도
힙을 이용한 다익스트라 알고리즘은 O(ElogV)의 시간 복잡도를 가집니다.
여기서 E는 그래프의 간선 개수, V는 그래프의 노드 개수를 의미합니다.
다익스트라 알고리즘의 핵심적인 알고리즘인 while 반복문은 노드의 개수만큼 수행될 수 있습니다.
while len(heap) > 0:
current_dis, current_node_idx = heappop(heap)
# 방문했다면 패스
if current_node_idx in visited_set:
continue
최악의 경우 그래프 내의 모든 노드를 큐에 넣고 꺼내는데
한 번 확인한 노드는 다시 확인하지 않기 때문에, 노드의 개수만큼 반복될 것 입니다.
# 인접 노드 최소 거리 갱신
for near_node in ad_list[current_node_idx]:
min_dis[near_node] = min(min_dis[near_node], current_dis + 1)
좀 더 구체적으로 보면, 그렇게 꺼낸 노드에 대해 노드가 가지고 있는 모든 간선을 확인하고 있습니다.
# 힙에 넣자.
heappush(heap, (min_dis[near_node], near_node))
그 후 노드 V의 모든 간선에 대해(정확히 말하면, 간선의 목적지에 대해) 다시 힙에 넣고 있습니다.
즉, 쉽게 말하면, 다익스트라 알고리즘은 그래프가 가지고 있는 모든 간선 E만큼 힙에 넣고 빼는 것과 유사한 연산을 진행합니다.
힙은 한 번 정렬 시 O(logN)의 연산을 하는데
데이터의 개수가 N개라고 할 때, 이를 N번 반복하므로 힙정렬은 O(NlogN)의 연산을 가집니다.
이를 통해 다익스트라 알고리즘은 힙에 모든 간선 E개를 넣어 정렬하므로 O(ElogE)개의 시간 복잡도를 가진다고 볼 수 있습니다.
간선 E의 최대 개수는 모든 노드가 서로를 향해 단방향 간선을 가지고 있는 것이므로 V^2개가 됩니다.
O(Elog(V^2)) = O(2ElogV) = O(ElogV)이므로, 다익스트라 알고리즘은 O(ElogV)의 시간복잡도를 갖게 됩니다.
Reference
이것이 취업을 위한 코딩 테스트다 with 파이썬 - 최단 경로 & 기타 그래프 이론
'알고리즘 > 알고리즘' 카테고리의 다른 글
| 비트 마스킹(Bit Masking) (0) | 2023.04.14 |
|---|---|
| 플로이드-워셜(Floyd-Warshall) (0) | 2023.04.13 |
| 순열(Permutation)의 코드화 (0) | 2023.04.05 |
| 조합(Combination)의 코드화 (0) | 2023.04.05 |
| DAG와 위상 정렬 (Topological Ordering) (0) | 2022.03.20 |
