출처 : 프로그래머스 코딩테스트 연습, https://programmers.co.kr/learn/courses/30/lessons/12953
코딩테스트 연습 - N개의 최소공배수
두 수의 최소공배수(Least Common Multiple)란 입력된 두 수의 배수 중 공통이 되는 가장 작은 숫자를 의미합니다. 예를 들어 2와 7의 최소공배수는 14가 됩니다. 정의를 확장해서, n개의 수의 최소공배
programmers.co.kr
풀이
def solution(arr):
#100 이하의 모든 소수 구하기
prime = set(range(2, 100))
for i in range(2, int(100**0.5) + 1):
prime -= set(range(i*2, 100, i))
prime = list(prime)
#소수 별 최대 지수값 기록을 위한 list
exponent = [0] * len(prime)
#숫자 소인수 분해
for num in arr:
count = 0
index = 0
while num > 1 or num >= prime[index]:
if num % prime[index] == 0:
num //= prime[index]
count += 1
else:
if exponent[index] < count:
exponent[index] = count
count = 0
index += 1
if exponent[index] < count:
exponent[index] = count
#소인수 분해 결과값으로 정답 구하기
answer = 1
for index in range(len(prime)):
answer *= prime[index]**exponent[index]
return answer
로직의 핵심은 모든 수를 소인수 분해한 후 각 소수별 최대 지수를 찾아서 전부 곱하는 것.
1. 100 이하의 모든 소수를 구한다.
2. 소수별 최대 지수를 기로하기 위한 list를 선언한다.
3. arr에서 숫자(num)를 하나씩 가져와서 소인수 분해한다.
4. 소인수 분해 시 2부터 작은 순서대로 늘려가며 소수별로 나머지가 0이 아닐 때까지 나누고 나눈 횟수를 count한다.
5. 더 이상 나머지가 0이 아니면 소수별 최대 지수와 count를 비교 후 큰 수로 update하고
count를 0으로 초기화한 후 다음 소수로 나누기 시작
6. num이 1이 되면 탈출하고 마지막 count에 대해 업데이트 해준 후 다음 num을 불러옴.
7. 반복
8. for이 끝나면 prime과 exponent를 불러와 prime의 exponent제곱을 모두 곱해 정답 도출
시간 복잡도
-
다른 사람의 풀이를 보면서 알게 된 점
- 최대 공약수(gcd)와 최소 공배수(lcm)의 관계를 이용한 풀이
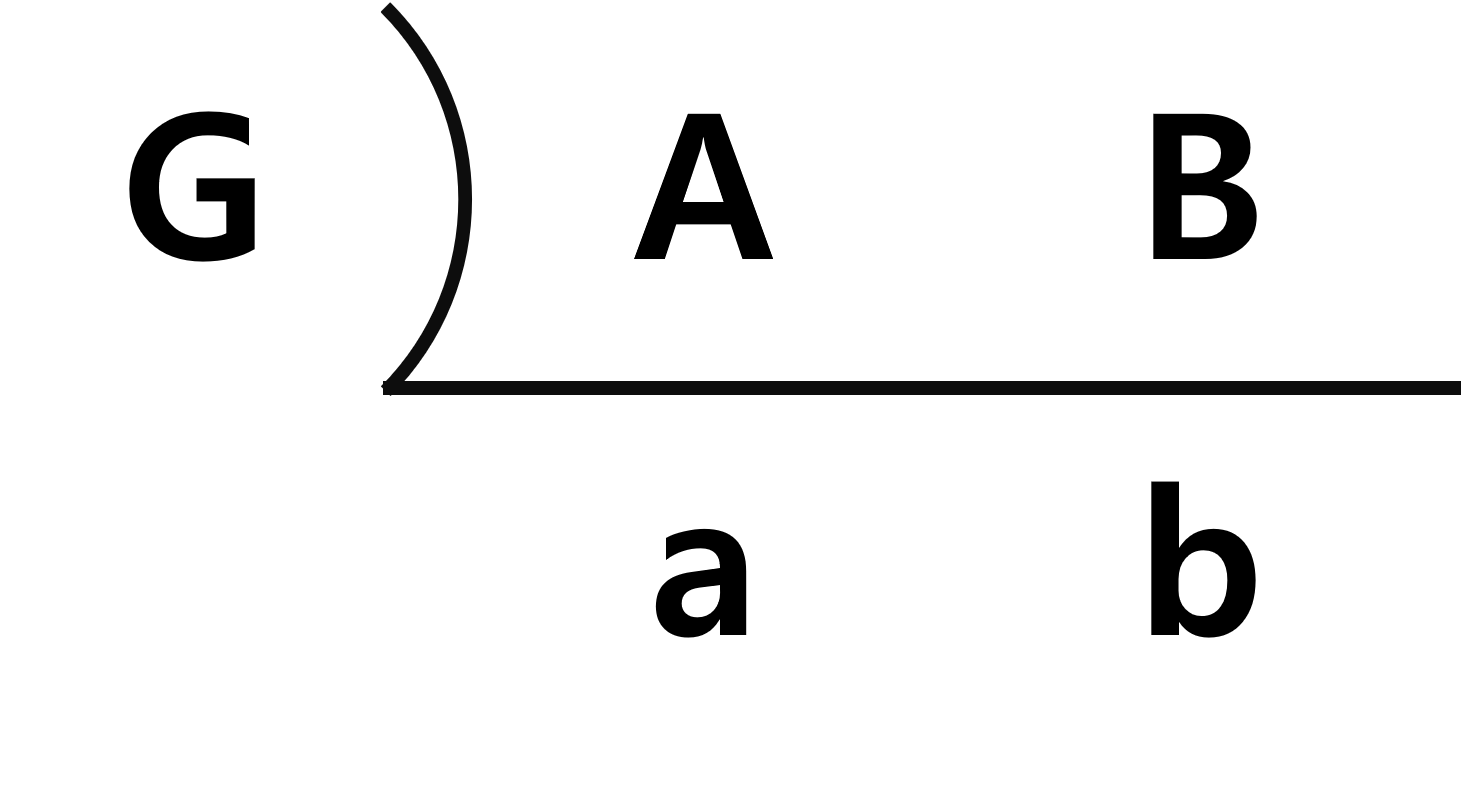
최대 공약수 G, 최소 공배수 L 이라고 하면,
L = G x a x b
A x B = L x G
이다. 이 관계를 바탕으로 다시 로직을 짜보면
1. A와 B의 최대 공약수를 구한다.
2. 이를 이용해 A와 B의 최소 공배수 L1을 구한다.
3. L1와 C의 최대 공약수를 구한다.
4. 이를 통해 L과 C의 최소 공배수 L2를 구한다.
5. 반복
import math
def solution(arr):
L = 1
for num in arr:
G = math.gcd(L, num)
L = (L // G) * num # G * a * b
return L
gcd 함수를 따로 구현해보면,
1. A의 약수를 모두 구함.
2. A의 약수 중 B로 나누어 떨어지는 것의 최대값을 구함
3. 최대값을 return
def gcd(A, B):
divid_A = []
for divid in range(1, int(A**0.5) + 1):
if A % divid == 0:
divid_A.append(divid)
if divid != A // divid:
divid_A.append(A // divid)
divid_A.sort(reverse=True)
for divid in divid_A:
if B % divid == 0:
return divid
- 유클리드 호제법
최대 공약수를 구하는 또다른 방법
16과 6의 최대 공약수를 구한다고 가정하면
16 = 6 * 2 + 4
6 = 4 * 1 + 2
4 = 2 * 2 + 0
즉, A를 B로 나누었을 때 나머지를 C라고 하면, B를 다시 C로 나누면서 나머지가 0이 될 때까지 반복하는 방법이다.
나머지가 0일 때의 나누는 수(이전의 나머지)가 최대 공약수가 된다.
def solution(A, B):
if A % B == 0:
return B
return solution(B, A % B)
고찰
알고리즘에서 수학적 지식이 중요한 이유...
'알고리즘 > Python' 카테고리의 다른 글
| [python] 프로그래머스 - 주차 요금 계산 (0) | 2022.03.01 |
|---|---|
| [python] 프로그래머스 - 괄호 회전하기 (0) | 2022.02.28 |
| [python] 프로그래머스 - 거리두기 확인하기 (0) | 2022.02.26 |
| [python] 프로그래머스 - 게임 맵 최단 거리 (0) | 2022.02.26 |
| [python] 프로그래머스 - 124 나라의 숫자 (0) | 2022.02.21 |
