본 글은 인프런의 영리한 프로그래밍을 위한 알고리즘 강좌를 듣고 정리하는 글입니다.
DAG (Directed Acyclic Graph)
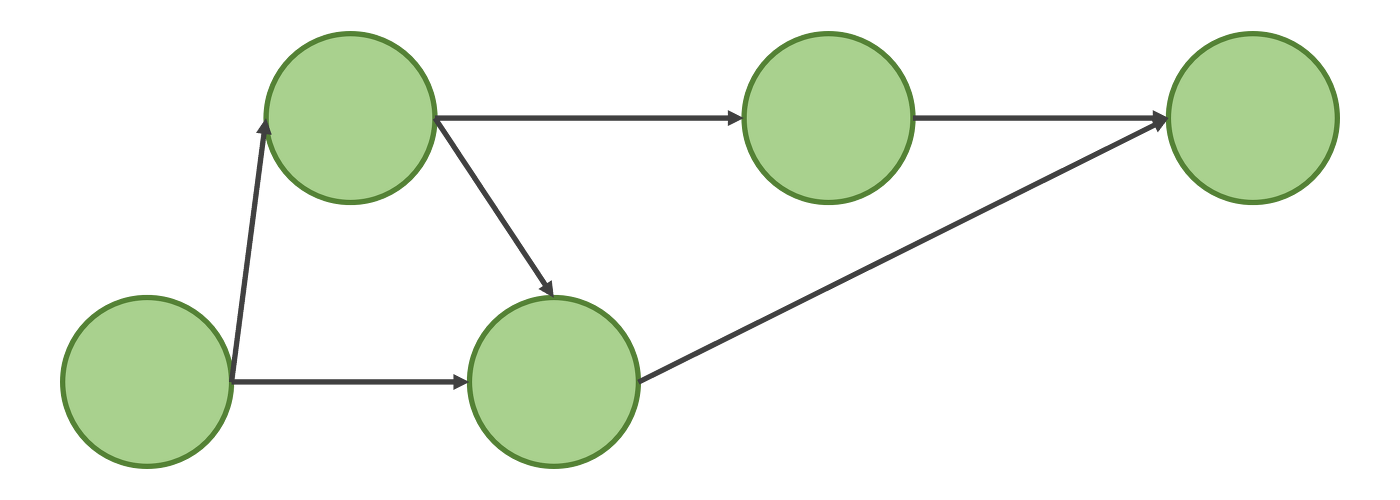
Directed : 방향성 있는
Acyclic : 싸이클이 없는
Graph : 그래프
즉, 싸이클이 없는 방향 그래프를 의미한다.
이를 만족하기 위해서는 모든 방향이 한쪽으로만 향해야한다.
작업의 순서와 같은 알고리즘을 표현할 때 주로 사용된다.
위상 정렬 (Topological Ordering)
위상 정렬은 그래프를 순서대로 시작점부터 종점까지 나열하는 정렬을 말한다.
BFS와 DFS는 무방향 그래프와 방향 그래프 모두에게 적용 가능하지만 위상 정렬은 DAG에만 적용될 수 있다.
위상정렬을 구현하는 방법으로는 2가지가 있는데
1. Incomming Edge(노드로 들어오는 엣지)가 없는 노드를 List 뒤에 추가하고 이 노드와 연결된 Edge를 모두 제거한다.
2. 반복
하는 방법. 이 방법을 생각할 때 생각해볼만한 것이 3가지 정도 있는데,
1. indegree(노드로 들어오는 엣지의 개수)가 0인 노드가 없다면?
-> indegree가 0인 노드가 없다면 싸이클이 존재하는 것이므로 위상 정렬 사용 불가
2. indegree가 0인 노드를 찾는 데에 시간이 걸린다.
3. 엣지 제거를 코드상으로 어떻게 구현할 것인가.
정도를 생각해볼 수 있다.
두 번째 방법으로는,
1. 빈 Linked List를 만들고 임의의 노드를 선택한다.
2. 선택한 노드로부터 DFS하며 방문 체크
3. 더 이상 방문할 수 있는 노드가 없는 노드에 대해 Linked List 앞에 추가한다.
4. 반복
하는 방법이 있다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| 순열(Permutation)의 코드화 (0) | 2023.04.05 |
|---|---|
| 조합(Combination)의 코드화 (0) | 2023.04.05 |
| BFS와 DFS (0) | 2022.03.20 |
| Dynamic Programming(동적 계획법) (0) | 2022.03.16 |
| Recursion(재귀) (0) | 2022.02.24 |
